
The last demo page mentioned that Daala's use of lapped transforms affects multiple aspects of the codec's structure. Classic intra-frame prediction is one example of a Catch-22 caused by lapping: We can't predict from neighboring pixels that have not yet been fully decoded, and we can't finish decoding these pixels until we lap them with the current block, which of course can't be decoded until after prediction.
To unravel this circular dependency, Daala predicts from neighboring frequency coefficients rather than neighboring pixels. This strategy also makes use of a larger amount of prediction information, as it predicts from several full blocks of coefficients, rather than a thin strip only one or two pixels wide.
As we code (and decode) the frames of a video block by block, we try to predict the contents of the each block as accurately as possible from previously decoded information; the closer we come to perfect prediction, the fewer bits we need to code the remaining difference. Prediction falls into two major categories: Inter-prediction, which predicts the contents of a block based on image data from previous frames, and intra-prediction, which predicts the contents of a block from neighboring blocks previously decoded in the current frame.

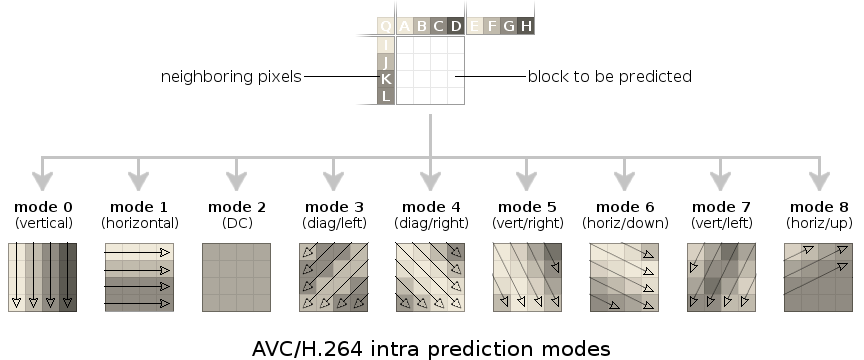
Above: Simplified diagram of spatial intra prediction as implemented in modern video codecs. The block to be encoded/decoded is predicted by one of several directional filters from a strip of pixels belonging to neighboring blocks that have already been decoded.
Due to mixtures of multiple blocksizes and other coding concerns, the coding order in a practical codec is usually more complicated than a raster scan of a single blocksize. Daala, for example, codes 32x32 superblocks in raster order, then 16x16 blocks within the superblock, then 8x8 blocks within the 16x16 block, then 4x4 blocks within the 8x8 blocks.
The simplest form of intra-prediction only predicts the DC coefficient of each block. Block-based image codecs have used DC prediction from the very beginning, and because the DC coefficient accounts for most of a typical block's energy, even a simple DC predictor (such as reusing the previous block's DC value) dramatically improves coding efficiency. Of course, more complex DC predictors can yield even better performance.
In addition to DC, AVC/H.264 introduced directional intra prediction in which the predictor extends the pixel values of a surrounding one-pixel-wide strip into the current block in one of eight signaled directions, aka coding modes. VP8 adds a tenth 'TrueMotion' mode (so named for historical reasons; it actually predicts gradients). HEVC also extends the prediction mechanism, adding additional modes, progressive prediction, and predicting from a larger two-pixel-wide strip.
Lapped transforms complicate the design of a successful spatial-domain directional predictor as exists in these other codecs. Directional intra-prediction relies on neighboring pixels that have already been decoded. Lapping complicates the idea of what 'neighboring' really means. In addition, neighboring blocks themselves aren't fully decoded without adding in the lapped values from decoding the current block. To decode the current block, we need to predict the current block, and predicting the current block lands us back at the beginning again. We need to break this circular dependency.
There are several obvious ways to relax the prediction constraints here, however most of the obvious tactics damage predictor efficiency. This is important to consider, because the efficiency advantage of a directional predictor can be tenuous to begin with. Despite offering eight directional prediction modes, for example, we see in testing that good H.264 encoders (such as x264) mostly use the DC-prediction mode. It's usually still the most efficient.
A damaged directional/spatial predictor may be worse than no predictor at all.
Daala predicts frequency coefficients in the frequency domain, rather than pixels in the spatial domain. Frequency coefficients are not shared between blocks, allowing us to keep the classic definition of 'neighboring' as well as avoiding any circular decoding dependencies. In addition, Daala's frequency-domain prediction draws from a larger input data set consisting of up to four complete blocks. In theory, the additional degrees of freedom could give us a more efficient predictor.
The frequency domain predictor is simple. We arrange the coefficients of the four neighboring, already-decoded blocks into a single vector. This vector is multiplied by a single linear predictor column vector to produce each predicted coefficient. We use a different linear predictor for each predicted coefficient, and so the complete block prediction is a matrix multiplication of the coefficient vector by a linear prediction matrix in which each column is one output coefficient's predictor.
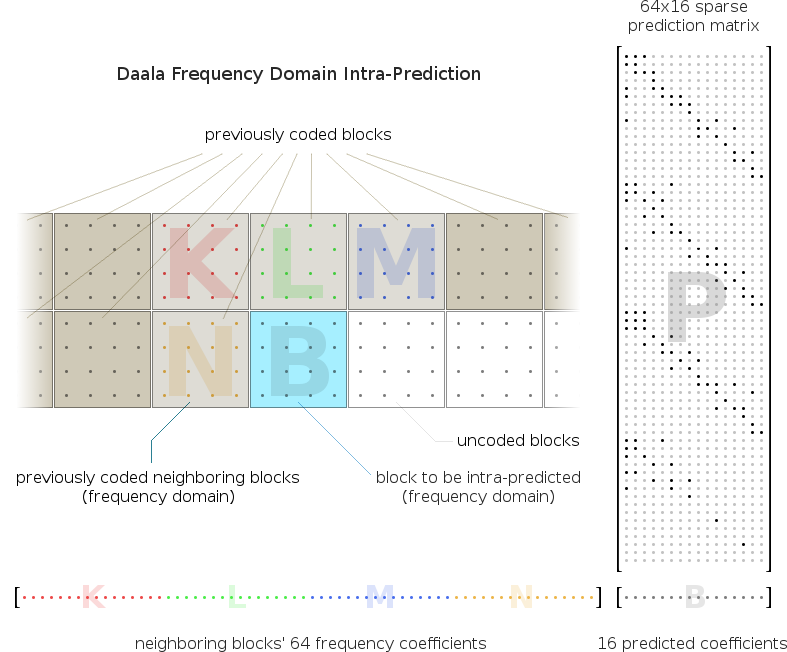
Above: Illustration of the Daala intra predictor for the 4x4 block case. The frequency-domain coefficients for the four blocks (K, L, M, N) neighboring the block to be predicted (B) are arranged into a 64 element row vector. This vector is multiplied by a sparse 64x16 linear prediction matrix (P) to yield the sixteen coefficients for the predicted block. As in other codecs, Daala supports multiple block prediction modes; each mode requires a separate prediction matrix.
Note that this diagram does not address coding order considerations; take as given the block to be predicted has four fully coded/decoded neighboring blocks of the same 4x4 blocksize.
There's a few things worth noting in this scheme. First, if we were not using a lapped transform, we'd be able to construct a frequency-domain predictor equivalent to the spatial predictor. From that it follows that the frequency domain predictor would be guaranteed to be no worse than the spatial predictor. Unfortunately, we don't have any such guarantee in the lapped case; the frequency predictor results may be better or they may be worse than the spatial case. Second, the matrix multiplication would appear to be large and expensive for a video codec. However, the frequency domain tends to be sparse overall; that's why we're coding in the frequency domain to begin with. We expect the predictors should be sparse as well.
Given the structure of the frequency-domain predictor, we still have the problem of finding a suitable matrix P for each mode in each blocksize. For purposes of proving this crazy scheme works, we tried something relatively easy first: a machine-training algorithm that turns out to be a kind of k-means clustering.
Assume we want to train ten coding modes, beginning with the ten VP8 prediction modes as a starting point. The first pass of our training algorithm classifies each block of a given size according to the starting VP8 coding mode with the lowest L1 (summed absolute) error in the frequency domain. We then compute a predictor for each output coefficient of each mode via a least-squares fit to the frequency-domain coefficients across the complete training set. This yields an initial set of frequency-domain intra predictors.
We then repeat this process using our newly trained predictors to classify the input blocks rather than the initial VP8 predictors. We continue iterating, using each run's new predictors to classify blocks for the next iteration.
After several such non-sparse iterations, we then sparsify the predictor; in the 4x4 case, we drop the 16 coefficients from P that contribute least to coding gain. Then we resume iterating. The numbers 10 and 16 here are obviously rather arbitrary; we're still exploring the solution space. However, we've now produced some early 4x4 and 8x8 predictors that prove the basic concept is workable (due to computational complexity, we've not been able to spend adequate time training the 16x16 case, so our 16x16 predictors are still loltastic).
Unlike H.264, VP8 or other codecs, the resulting modes don't really 'mean anything'; they're just the results of machine training. That said, the modes do show some recognizable spatial qualities. Some interesting training points:

Above: Interactive demonstration of Daala's frequency-domain prediction for the 4x4 block case. Use the mouse to set a single pixel or frequency coefficient to a positive value to inspect the predictors' spatial and frequency domain reactions. Clicking a coefficient will freeze the display on that result; The Escape key unlocks the display so that the cursor resumes following the mouse pointer.
The spatial input on the upper left-hand side accounts for lapping, so the input area that affects a given block's frequency coefficients extends by half a block into its neighboring area. It is this overlap that complicates our ability to perform prediction in the spatial domain, and motivates Daala's use of frequency-domain prediction.
The basic visual qualities of Daala's prediction are somewhat different from other codecs. Spatial directional prediction achieves low error in the spatial domain, but tends to overlay a strongly directional texture on top of whatever natural texture exists in the image. As a result, the residual is usually a mixture of the multiple spatial textures with much of the error in high frequencies. Daala optimizes prediction error in the frequency domain, so the resulting residual tends to look more like a mask of the original image. It remains to be seen if this difference is a perceptual advantage, liability, or neither.
| Predictor Output | Prediction Error |
 |
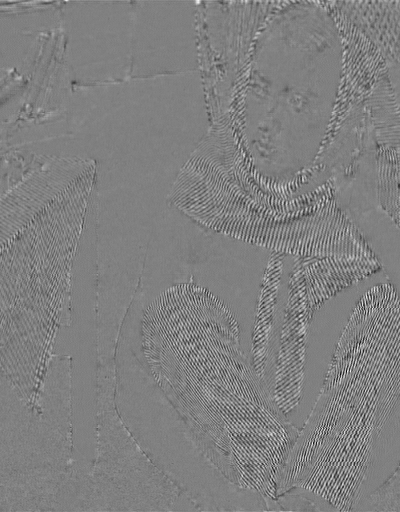 |
Above: An interactive illustration of the output of Daala's frequency-domain intra prediction and VP8's spatial-domain intra prediction for 4x4, 8x8 and 16x16 blocks over a small number of images. The 4x4 and 8x8 Daala prediction shown is from training as of July 23, 2013. The 16x16 images were updated on October 3, as the earlier 16x16 prediction was mostly untrained.
The predictors seen here are likely to see significant improvement as we explore more of the solution space. Despite this, the combination of lapped transform plus our proof-of-concept grade frequency-domain prediction currently delivers higher coding gain than a DCT + VP8 spatial predictor.
Remember when comparing images above that this is the output of the predictor, not the encoder. The prediction doesn't have to look good, it only has to reduce the number of bits to encode.
A complete prediction system must account for a number of logistical complications that we've ignored so far. These fall into two basic categories: Missing data and mixed block-sizes.
In a given coding scheme, we're not always going to have four full neighboring blocks available for prediction. Accounting for all possible factors and considering multiple potential coding orderings, we're going to be missing some information approximately 1/3 of the time. Proofing against missing information can be built into the training; by using training conditions as close as possible to actual encoding, the resulting predictors can cope with missing information. We simply ignore the blocks that don't exist (or potentially use alternate predictors trained for that case).
Multiple blocksizes also complicate prediction. We cannot have a predictor set for every possible neighboring blocksize combination; the combinatorics grow out of control. Thus we need to determine the best way to homogenize prediction when using multiple blocksizes, even in the case where neighboring blocksizes are mixed.
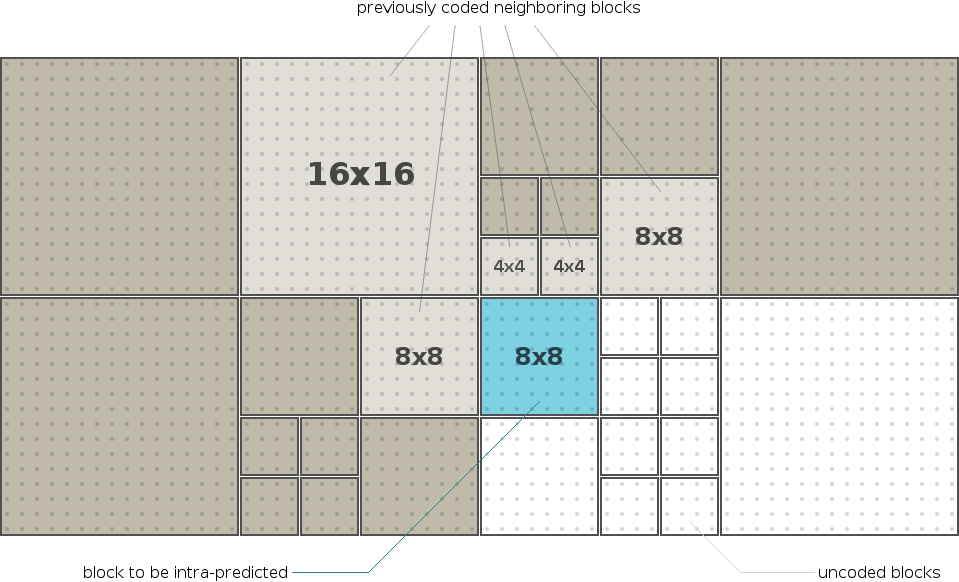
There are a couple different strategies for this, but they all rely on being able to alter blocksizes after the fact, something I haven't mentioned yet. To do this, Daala borrows a technique from Opus for combining and splitting transformed blocks that we refer to as Time-Frequency Resolution Switching, or TF for short.
That's for the next demo (now posted), so stay tuned :-)
—Monty (monty@xiph.org) July 23, 2013