

aala is a new general-purpose video codec currently under development at Xiph.Org. Our performance target is roughly a generation beyond current 'next-generation' codecs like VP9 and HEVC, making Daala a next-next-generation effort. As with other Xiph codecs, the Daala format is and will always be royalty-free with a permissive FOSS license.
On May 30th 2013, our in-development Daala prototype encoded and decoded its first streams. Two hours later, Mozilla's David "oneman" Richards streamed the first live Daala video over the Internet. Although the project is still pre-pre-alpha, I think it's time to introduce Daala to the world.
The next-generation VP9 and HEVC codecs are the latest incremental refinements of a basic codec design that dates back 25 years to h.261. This conservative, linear development strategy evolving a proven design has yielded reliable improvement with relatively low risk, but the law of diminishing returns is setting in. Recent performance increases are coming at exponentially increasing computational cost.
Daala tries for a larger leap forward— by first leaping sideways— to a new codec design and numerous novel coding techniques. In addition to the technical freedom of starting fresh, this new design consciously avoids most of the patent thicket surrounding mainstream block-DCT-based codecs. At its very core, for example, Daala is based on lapped transforms, not the traditional DCT.
...so let's start there.
Modern codecs typically encode video at bitrates that work out to substantially less than one bit per pixel. They do this by grouping pixels together, typically into 4x4, 8x8 or 16x16 blocks, then transforming the blocks with a two-dimensional Discrete Cosine Transform (DCT).
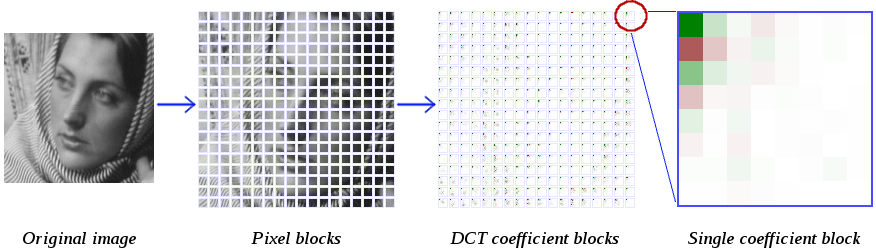
The DCT converts the blocks of pixels into same-sized blocks of frequency coefficients. It also compacts most of the energy from the original pixels into just a few coefficients, arranged such that reduced precision in the frequency domain is far less noticeable than reduced precision in the spatial domain. Thus, the DCT makes it possible to encode the image in less space, as the most important aspects of the image are represented in a more compact form.
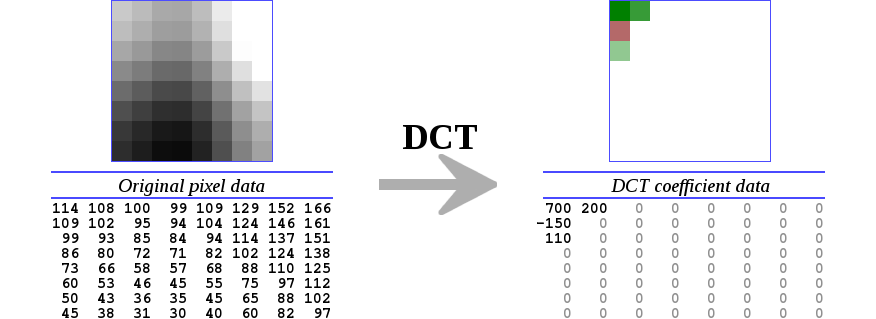
An encoder then quantizes the DCT coefficients to a lower precision, usually via a complex heuristic algorithm that's been carefully tuned. Let's handwave that away for now, and do the simplest possible thing: quantize all the coefficients by a fixed quantizer. The decoder then uses an inverse 2D DCT to reconstruct the original image block by block.
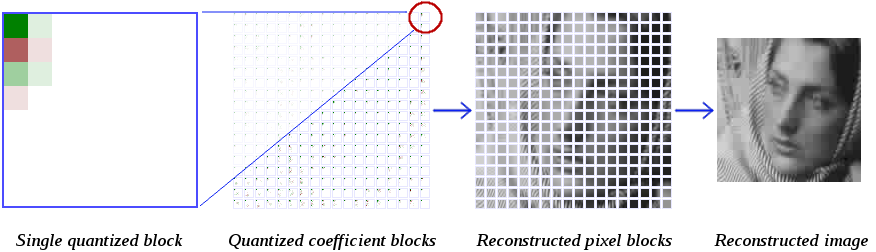
There's an obvious change here; we can clearly distinguish the sharp boundary of each individiual block in the reconstructed image. A DCT is a circular [edit: braino there, I meant symmetric not circular] transform, and so the block edges introduce strong discontinuities. When we invert the transform, the spatial error introduced by quantization causes the block edges to no longer 'line up'. Average spatial error is also greater at the block edges, which further exacerbates the problem.

For this reason, virtually all video codecs use a deblocking filter to smooth over the edges between blocks. This filter may be a purely post-processing step, or it may exist within the encoding loop in which case it's called a loop filter. This filter began life decades ago as something of an afterthought, but it's an integral part of modern codecs accounting for a significant portion of the design complexity and CPU cost.
A deblocking filter is at best a necessary evil. It discards legitimate detail at block edges at the same time it smooths the boundary discontinuities. Further, the details the deblocking filter unintentionally discards cost bits and CPU time to encode. Finally, good deblocking filters are complex and heuristic, requiring detailed analysis (and in some cases, additional signaling) to control conditional application. The heuristics have become quite good, but they can go wrong.
A lapped transform renders this necessary evil unneccessary. It has some other nice benefits as well.

A lapped transform is any transform where each block overlaps its neigboring blocks. Audio has used overlapping transforms since approximately forever; the best known example is the Modified Discrete Cosine Transform (MDCT) that powers MP3, Vorbis, AAC, and Opus. Many other transforms also fall under the 'lapped transform' definition (and it's important to point out Daala does not use the MDCT), so let's be more specific.
First, consider a deblocking filter that's invertible; a wide variety of such filters are possible, if not widely used. Next suppose that the inverse of the deblocking filter is applied before the forward transform as a pre-filter P, and the deblocking filter is applied after the inverse transform as a post-filter. If we use the DCT as our transform as above, the pre-filter + DCT is now perfectly inverted by the inverse DCT + post-filter.
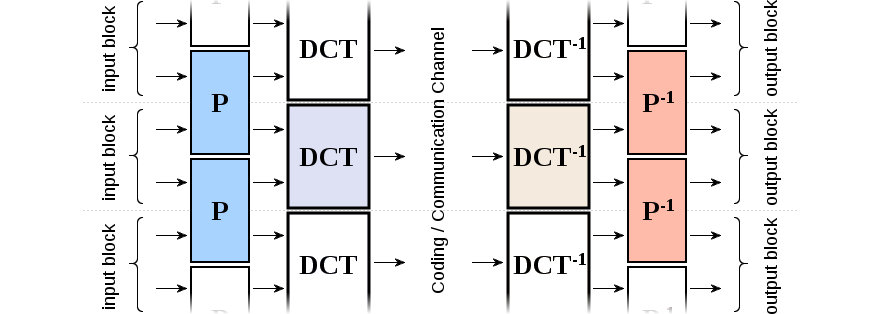
The post-filter is similar to our deblocking/smoothing filter from earlier. The prefilter is the inverse, so it's literally the opposite; it purposely makes the input image very blocky by reducing the circular discontinuity at the edges. When paired with the DCT, this means it compacts more energy into the DC component by reducing energy leakage into higher-frequency bins.

The remaining goal is to find a specific P (and P-1) that, along with the DCT, forms a new lapped transform with the visual, coding, and computational properties we desire.
Using spatial-domain lapping and lapping transforms for images and video is not a new idea, even if it's not mainstream. Papers on the subject date back to Malvar et. al. in the early 1990s, so we have a decent amount of preexisting research to draw upon.
Lifting filters are another idea that's not new, though they are relatively recent. Originally a product of wavelet transform research, the generalized idea is powerful: A lifting filter is comprised of sequence of serialized lifting steps also simply called lifts. Each step updates a single variable xi in place from an arbitrary function f() that does not depend on xi. That is:
The function f() is usually quite simple, e.g. just one other value scaled. Lifting steps are often arranged in alternating lifts where value xa is updated from value xb, and then value xb is updated from value xa. The literature often refers to the alternating lift steps as 'predict' (P) and 'update' (U or Q) steps as a result of their origin in second-generation wavelet transforms.
A lifting filter is always exactly reversible; the steps can simply be unwound in the opposite order.
Daala uses pre/post lifting filters based on the filters proposed by Tran, Liang, and Yu in Lapped Regularity-Constraind Pre- and Post-Filtering for Block DCT Based Systems. The prefilter P consists of forward and inverse lifting butterflies and transform matrices U and V. It turns out that U and V duplicate each others' degrees of freedom, so we set U to the identity matrix and eliminate it from the filter design.
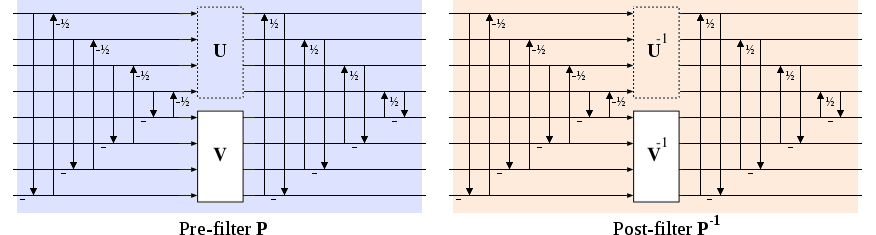
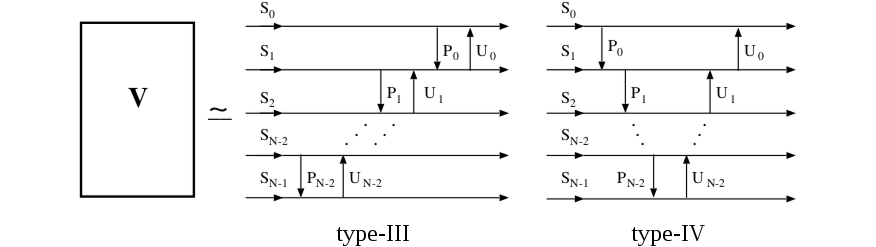
Research literature suggests several possible models for matrix V; the 'type-III' and 'type-IV' models allow easy lifting implementations that suit our desired transform structure. These simplified models allow selection and optimization of the parameters via nonlinear optimization techniques or even exhaustive search.
The DCT itself can also be implemented via lifting, and we've implemented one with both perfect reconstruction and orthonormal scaling. Placed together with the pre-filter, we can implement the entire forward lapped transform as a complete lifting structure.
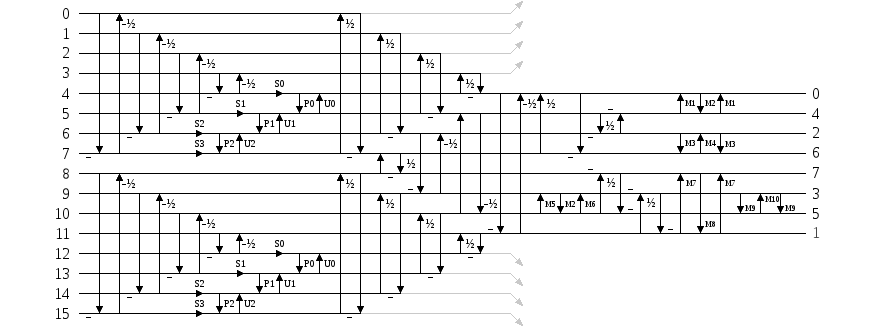
As any lifting filter is inherently invertible, constructing the inverse transform is a purely mechanical process. Lifting also makes it trivial to implement exact reconstruction as an integer transform. Quantization error carried through the forward transform is exactly reversed in lock-step fashion by the inverse transform. This can both dramatically reduce required numeric resolution (Daala's filters currently use six-bit coefficients) and also opens the possibility of fully lossless operation.
In the next demo (update: now ready!), I'll continue exploring some of the interesting new (or at least, non-mainstream) techniques used in Daala. There's more to cover regarding implications of the lapped transform, and that leads nicely into frequency-domain intra prediction.
—Monty (monty@xiph.org) June 20, 2013