
The first Ghost update was an introduction and overview of the underlying codec structure under research for Ghost. First and foremost among structural novelties, Ghost is to be a hybrid time/frequency codec that splits and separately encodes tonal and atonal content. Though not a new idea, hybrid encoding use in a practical general purpose audio codec is somewhat novel (for several good reasons). Part of the purpose of Ghost is to reevaluate hybrid coding to see if any new discoveries make the hybrid approach more advantageous.
In this update, we look at details of our frequency-domain analysis and representation.
The FFT (Fast Fourier Transform) and similar related transforms that offer smooth overlapping blocks (such as the MDCT) are all transforms that map a time-domain signal into the frequency domain, that is, a summed series of a fixed set of sinusoids. These transforms are 'critically sampled', meaning that N time domain input samples yields N output sinusoidal amplitude values; the number of values in equals the number of values out. They are also (at least) bi-orthogonal; the process is lossless and can be reversed exactly.
The FFT is a remarkable transform and offers such a level of mathematical convenience and power that it is pressed into service as a way of optimizing or approximating countless other transforms. It is a big enough hammer that at some point, every signal processing problem starts to look like just another nail (or one of your thumbs).
Because the audio we hear is, in a sense, a series of summed sinusoids, the FFT (or more commonly today, the closely related MDCT) also seems ideal as a good transform space for near-ideal representation of audio signals, usually offering substantial energy compaction over the time domain. The frequency domain is close enough to how audio 'really works' it's been the default coding domain for audio for over twenty years. Though very close, it is not a perfect fit.
Fixed-basis discrete-time Fourier transforms like the FFT and MDCT have some limitations when used for audio. Not all sounds are composed of a small or neat series of sinusoids; many are not periodic at all. Time->Frequency transforms are not 'causal'; quantization and coding error in the frequency domain spreads both backward and forward in time, causing pre and post-echo artifacts. Any sounds that are not a fairly simple sum of long-term steady-state sinusoids become a wideband spray of energy in the frequency domain, resulting in poor energy compaction and thus low coding efficiency.

Highly impulsive, compact sounds in the time domain show poor energy compaction in the frequency domain. In addition to low coding efficiency, quantization of the frequency domain values will cause the time-domain transient to spread in time resulting in pre-echo. Sharp transients are a traditional Achilles-heel of frequency-domain transform codecs.
Even neat, perfect sinusoids can run into representational trouble in the frequency domain. Sinusoids that are modulated in amplitude and/or frequency, or sinusoids that fall between bins (do not match one of the basis frequencies exactly) also become spread out across the entire frequency spectrum. Most of this energy spray is low energy, but collected in its entirety it is not negligible. Discarding this 'long tail' of leaked frequency-domain energy is responsible for the artifacts we hear in transform codecs.

The FFT can perfectly represent a signal in a single peak only when the signal is a sinusoid that exactly matches one of the basis frequencies ('hits a bin') and shows no frequency or amplitude variation.

When a sinusoid lands 'between' frequency bins, the FFT produces a main peak that straddles two bins as well as a spray of leakage that fills the rest of the spectrum with lower-energy values. Though most of the energy is still in a few values near the peak, a complete representation of this simple sinusoid now requires a large number of frequency-domain values.

Any change or drift in amplitude (amplitude modulation) in a sinusoid that otherwise perfectly hits a bin also causes energy leakage and spreading away from the central peak across the entire spectrum.
 Similarly, frequency increases or
decreases across a frame (frequency modulation or chirping)
also leaks energy like the other sinusoidal
'imperfections'. The faster the chirp (the faster the
frequency change) the less distinct the central peak and the
greater the full-spectrum leakage.
Similarly, frequency increases or
decreases across a frame (frequency modulation or chirping)
also leaks energy like the other sinusoidal
'imperfections'. The faster the chirp (the faster the
frequency change) the less distinct the central peak and the
greater the full-spectrum leakage.

The usual way of controlling energy leakage from 'imperfect' signals is to window the input signal using a function that itself shows low energy leakage; the effect of a Hanning window is shown here. This practice is effective at controlling but not eliminating energy leakage.

Windowing comes at a cost; the main peak of even perfect sinusoids is broadened and flattened. The already flattened and spread peak of a modulated sinusoid is further flattened and widened. This has the practical consequence of making it more difficult or impossible to distinguish sufficiently closely spaced signals.
In practice, this windowing tradeoff is necessary to achieve acceptable leakage rolloff, else low amplitude signals farther away from a strong peak will be completely swamped by a stronger peak's energy leakage.
What can we gain by relaxing the constraints imposed by a classic fixed-basis transform like the FFT and MDCT?
The first obvious constraint we can relax is the fixed, evenly spaced frequency basis, allowing representation of any frequency, not just sinusoids spaced a fixed distance apart. In short, we turn the FFT:
...into an arbitrary collection of sinusoids where
This obviously loses the critical sampling properties of the FFT in that a fixed number of input samples can turn into any number of output sinusoids. We also (in practice) lose bi-orthogonality, but we're not interested in exactly representing the time signal; we merely want a better fit to specific sinusoidal features of our choosing.
The generalization also eliminates the possibility of a directly calculated closed-form solution. We must use a general purpose linear system solver; such a solver calculates an approximation to a solution, inspects the error, and then uses the previous approximation and error to construct another, better approximation. This process repeats (iterates) until the approximation either achieves the desired level of precision or fails to converge on a stable answer.
We can add rate-of-change of the amplitude (essentially slow amplitude modulation) as a new axis of freedom to the sinusoidal fit:
(The above modifies the sinusoidal basis function to ramp up from zero amplitude, ramp down to zero amplitude, or anything in-between. When ΔA==0 and ω are restricted to integer values, it's the regular discrete Fourier transform.)
This is not new information to the analysis process as we can determine (and normally do determine) the same approximate amplitude change information using successive FFTs. However, adding frequency modulation as a fit parameter allows tighter modeling of a signal than determining an amplitude delta after-the-fact.
Strong periodic signals are often but not always fixed-frequency sinusoids. Audio also contains linear-frequency chirps, where the frequency changes linearly over time (these are also called 'quadratic' chirps as they're described by a quadratic formula). Log frequency chirps (with logarithmic frequency change over time) are an even more common occurrence in both music and audio in general. For convenience we can approximate log chirps with successive linear chirps.
Extension of the basis functions to cover arbitrary linear frequency chirps is straightforward:
We can generalize the discrete Fourier transform, which returns N amplitude values for N fixed, evenly-spaced sinusoids spanning from DC to the Nyquist frequency, with arbitrary chirps that have five real degrees of freedom: Amplitude, Phase, Frequency, Amplitude', and Frequency', where prime indicates first derivative. We could go further and add second derivatives or other tangentially related qualities. For now, we make the arbitrary decision that this 'feels like' a good set, and will be the basis of further research. Five degrees of freedom, none of them inherently quantized, already describe a large potential expansion of input information. Subject to subsequent research, it is more likely that five degrees is past the ideal number rather than short of it.
The FFT presents us with effectively three parameters per sinusoid:
The MDCT is similar, but the output is a vector of real amplitudes rather than complex amplitudes. The total number of output values remains the same. Despite the amplitudes all being real values, they exhibit left/right symmetries/anti-symmetries that behave similarly to complex pairs.
For both the FFT and MDCT, these values are a unique solution. For any given input signal, the basis frequencies and resulting amplitude outputs at each basis frequency are a fixed mapping. Note again that the frequencies are often implicit and the amplitudes simply listed in order for each basis frequency.
The chirp domain is simultaneously massively over- and under-determined. It is overdetermined in the sense that we have more fit axes/parameters than data points, but underdetermined in the sense that we're only interested in 'significant' fits, where the determination of what constitutes 'significant' is a problem left to the researcher.
Adding a single parameter (the frequency delta/modulation) to the Fourier transform converts the 1-D frequency domain mapping into a 2-D mapping with center frequency along one axis and frequency delta along the other. For a single chirp, the highest amplitude will be at the point along both axes corresponding to the chirp parameters. The sharp peak will flatten out as one moves away from the correct chirp rate along the frequency delta axis.
The first graph at the left illustrates the solution space with a single chirp. The top half of the graph is a spectrogram with frequency along the X axis and time progressing forward down the Y axis. The lower half is a plot of magnitude in the chirp space, with chirp center frequency along the X axis and chirp speed increasing downward along the Y axis.
Once the signal becomes complex (more than one sinusoid or more than one chirp, such as the voice sample in the second graph left), the sidelobe leakage that presents a simple bow tie pattern in the first graph becomes constructive or destructive depending on phase alignment. The resulting pattern becomes quite complex and it's not possible to simply choose the strongest local maxima as the 'correct' answers.
An FFT is able to provide a good-enough estimate of several parameters of a chirp fit. Specifically, the average amplitude, approximate center phase, and approximate center frequency of a chirp can be estimated directly from an FFT. We can estimate amplitude modulation from the results of two successive FFTs. The sticking point is estimation of chirp rate (frequency modulation). Once the chirp rate exceeds approximately .25-1.0 bins per FFT, which we expect it will on a regular basis in natural audio and music, estimation using successive FFTs becomes noisy and error-prone.
At this point, we notice that our sinusoidal estimation code exhibits a wider range of convergence when used with a good window than noted in our original 2007 paper. When coupled with a nonlinear iteration that recenters both frequency and chirp rate, both convergence and output precision improve further. In particular, the convergence range of the chirp rate parameter can be widened arbitrarily, which is an especially lucky break. It becomes perfectly practical to fit chirps using an initial chirp rate estimate of zero, letting the linear solver find the answer without additional hinting. In-depth details of sinusoidal estimator behavior including window effects will be the subject of the next update.

From our 2007 paper An Iterative Linearised Solution to the Sinusoidal Parameter Estimation Problem: "Region of convergence as a function of the sinusoid frequency. The algorithm never converges when the initial estimate is off by more than 1.05 DFT bins (2π/L rad/s)."
This graph turns out to be so incomplete as to qualify as effectively incorrect. The specific window in use, the given input signal, the initial fit estimate, and myriad other minor modifications to fit conditions or technique all exert substantial influence on convergence behavior.
Tl;dr: Ignore the graph on the left. It's useless. Next update, we'll have substantially more useful data.
The sinusoidal estimation has an additional advantage over a brute-force DCFT-style approach; because it fits in order of estimated energy, it tends to reduce the interference from sidelobe leakage. This reduction of sidelobe pollution, coupled with the fact that most chirps evolve from stable frequencies (or move slowly) appears to result in more than adequate performance from simply using an initial fit estimate of zero for the chirp rate.
Exceptionally tight chirp fitting potentially allows better energy compaction into fewer parameters, more than offsetting the fact parameter expansion means we'll need to code more data per sinusoid (It's a lovely theory in any case). This is a benefit to accurate audio analysis, allowing us to account accurately for more signal energy, even if we decide to discard or degrade the additional precision when coding rather than coding the full depth.
Tight chirp fits grant another benefit; the mechanism by which we fit chirps also becomes the mechanism by which we track chirps from frame to frame. We can extrapolate chirps forward (and backward) seamlessly following sinusoidal energy as it moves between frames and FFT bins. Forward extrapolation of a chirp from a preceding frame into the new frame becomes the initial estimate to the chirp fit estimation algorithm. This eliminates the need to search for the chirp all over again in a new frame, and then try to match it to a preexisting chirp from earlier.
Left: A synthetic chirp tracked frame-to-frame by the same sinusoidal estimation code that performs the initial fit. For each frame, the estimation code performs a new fit, extrapolating the previous frame's fit as the initial estimate for the current frame fit. In this mode, the estimator typically returns convergence in a single iteration.
The top half of the graph is a spectrogram showing frequency on the X axis and time moving forward down the Y axis. The purple shows FFT output and the white line shows the chirp estimation code precisely tracking the chirp through time.
The lower half shows a graphic representation of the spectrum of the latest block of samples with frequency along the X axis and amplitude on the Y axis. The purple background is a plot of the magnitudes output from an FFT. The line marks the more precise frequency and amplitude found by the chirp fitting/tracking code for the same input block.
The practical tradeoff with going to a generalized chirp encoding is the expansion in the number and precision of parameters to encode. The hope is that better energy compaction into fewer chirps offsets the fact that each individual chirp is potentially more expensive to encode. That said, there are more and less expensive ways to encode chirps, some of which can reduce the additional expense while still potentially maintaining the advantages of the tighter fit. Only testing will tell.

Vorbis and other present-day monolithic transform codecs like AAC use the MDCT for their frequency domain transform. Such a codec will encode the logical equivalent of every MDCT output value in order to avoid coding frequency offsets, though coding will be optimized to assume many of the amplitude values will quantize to zero. Each frame's MDCT is stand-alone, meaning that when we eventually decode the frame, none of the data needed to reverse the MDCT transform relies on data from any other frames (though the output is overlapped with neighboring frames). No values are predicted across frames.
The amplitudes produced as output of an MDCT can be thought of as a specific, restricted set of Gabor atoms. Each amplitude and implicit basis frequency, along with our window function, describes a single Gabor atom. All the atoms are constrained to begin and end on a frame boundary, only atoms corresponding to the basis frequencies are possible, and the modulation parameters are always zero.
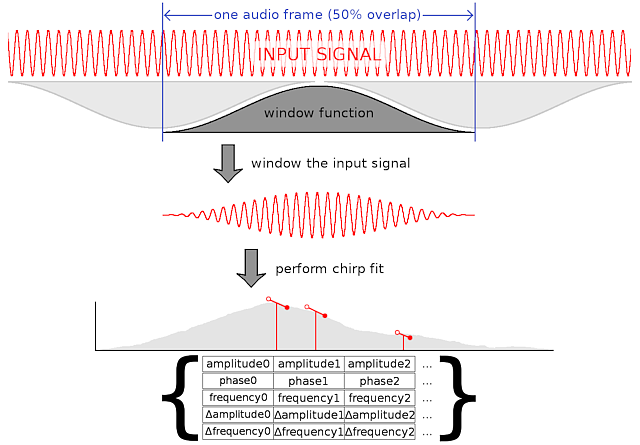
Viewing MDCT output as a highly-restricted set of Gabor atoms makes it clear that our proposed chirp fitting can be as simple as a relaxation of the constraints on the possible set of Gabor atoms we can choose to use. We still restrict atoms to beginning/ending on frame boundaries, but we no longer restrict the center frequency of the atom to a fixed basis set, nor do we clamp the modulation terms to zero.
This generalization allows us to code fewer sinusoids more precisely. The obvious tradeoff is that rather than our atoms being described by a single explicit parameter (a list of amplitudes), the atoms are now described by five explicit parameters.
As with the MDCT, a stand-alone frame requires that we do not predict or preserve any chirp parameter data across frames. We code into each frame all the data needed to reconstruct the time-domain signal.
We're not necessarily stuck coding five full-range parameters for every chirp. From frame-to-frame, most chirps will predict rather well a matching chirp in a following frame, a trick much harder to achieve with the MDCT. If we remove the requirement that frames must be strictly stand-alone (using no parameter information carried over from a another frame), we can use the chirp parameters from a preceding frame to predict the chirp parameters of the current frame, much like inter-coding in video codecs.

At the beginning of a new frame, we know the phase, amplitude and instantaneous frequency of a previous frame's chirp at the frame boundary (as well as across the portion of the previous frame that overlaps with the current frame). If we're content to eliminate some axes of freedom fitting a current frame chirp, we can reduce the number of fit parameters by fixing a current frame chirp to a preceding frame chirp at some point. For purposes of illustration, let's assume we're fixing the current chirp to the previous chirp at the starting boundary of the current frame.
Up to now, we've defined the phase, amplitude and frequency parameters at the center of the fit window. We now alter the chirp fit to interpret phase, amplitude and frequency parameters at the left boundary of the chirp rather than the center, then fit the current frame's chirp with these three parameters fixed to the values taken from the preceding chirp at the frame boundary.
As the left edge of the chirp is fixed, the things that can change across the frame are the amplitude and instantaneous frequency. Thus, we've rendered three of our five parameters for the new frame's chirps implicit, leaving only the need to fit the amplitude and frequency modulation across the current frame.
This two-parameter chirp arrangement still synthesizes chirps the same way as the five parameter chirps, using overlapped Gabor atoms. It merely borrows some chirp parameters from the preceding frame.
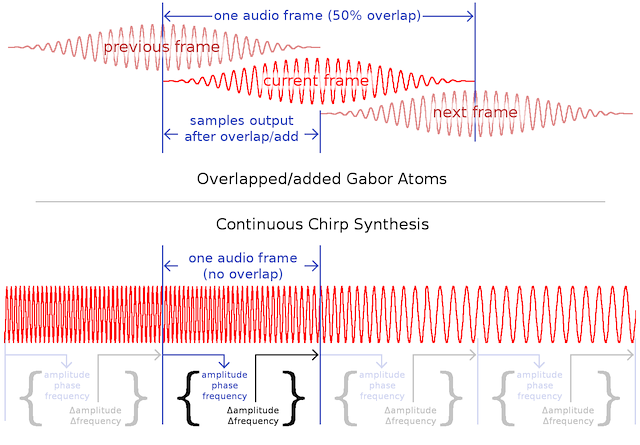
Rather than constructing and overlap-adding Gabor atoms, we can synthesize chirps directly from free-running oscillators, realizing a potential factor of two savings in synthesis cost. Analysis could be performed exactly as it is in the two-chirp arrangement with overlapping frames above, but the native synthesized frames would be half the size and non-overlapping.
Continuous chirp synthesis is not exactly equivalent to the overlap-add schemes above as we're no longer adding together overlapped chirp atoms with potentially disagreeing parameters.
In the case of independently constructed Gabor atoms, the process of sewing together frames is as straightforward as it is in the MDCT (which is itself just a special case of Gabor atoms). Just like in the MDCT we need only use a power complementary window, overlap and add.
Once we're constructing chirps from frame to frame as if they're the output of free-running oscillators, things become more complicated. We no longer have a smooth overlap/add window, and so we no longer have implicitly smooth transitions between sets of chirp parameters. Is piecewise linear chirp construction (discontinuous in the first derivative) sufficiently smooth for high fidelity reproduction? Or will additional transitional smoothing be necessary to move discontinuities into higher derivatives or eliminate them altogether?
Conceptually, there's no difficulty in constructing arbitrarily smooth transitioning between parameter updates. That said, smoothing increases computational complexity. In addition, smoothing not reflected in the original chirp fitting algorithm results in synthesized chirps that are not equivalent to the fitted parameters.
 Ghost development work is sponsored by Red Hat Emerging Technologies.
Ghost development work is sponsored by Red Hat Emerging Technologies.