the goal here: move edge (or feature) energy that's spread throughout the lapped-DCT transform domain into a constrained partition (or partitions) of coefficients.

the DCT transform (and lapped DCT transform) of a pixel-domain edge is itself edge-like, with transform energy spread out across coefficients throughout the transform domain.

The goal of traditional intra-prediction is to predict edges so that edge energy is substantially removed from the block, decreasing the number of important transform coefficients to code. Also, the HVS is very good at extracting and evaluating sharp edges, and the alternate prepresentation of edges (through prediction) in a way better suited to maintaining their sharpness and contrast is visually pleasing.

What I'm trying here post-facto modifies the effective bases of the lapped transform to represent directional edges (or perhaps even more complex features) such that all transformed energy from the edges is constrained to a subset of coefficients, such as the first row, first row/column, or first few PVQ partitions.

Hopefully, the constrained edge-energy coefficients will also simplify the computational complexity problem facing our frequency-domain intra prediction. We'll have fewer coefficients to predict, and likely fewer coefficients from which we need to predict. In addition, we may be able to infer coding modes from the coefficient subset, rather than signalling coding modes explicitly.

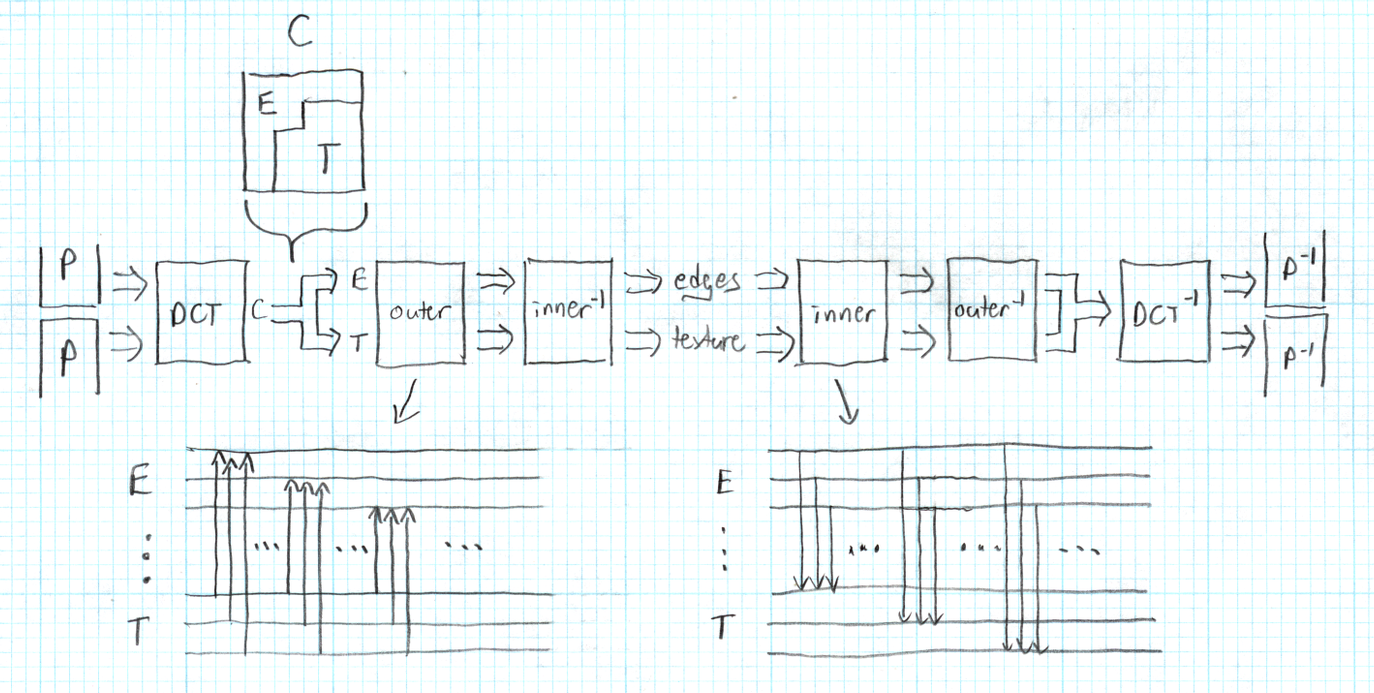
This is all implemented via a pair of lifting filters tacked onto the butt of the DCT.

The lapped DCT produces a block of coefficients C that we divide into two groups, E (edges) and T (texture). The 'outer' filter is a series of lifts from T to E. The 'inner' filter is a series of lifts from E to T. 'outer' is trained to copy edge energy from T to E. 'inner' is trained to copy edge energy from E back to T. The inverses remove the edge energy from E and T respectively.

Thus the forward DCT output is modified by running the coeffients through 'outer', which copies energy to E, and then the inverse of 'inner' which removes the copied energy from T. 'outer' followed by 'inner-1' thus move edge energy from T to E.

Synthesis is the inverse; after decoding, the coefficients are run through 'inner' and then 'outer-1', moving the edge energy back to its original coefficient locations.

Training is a little different:

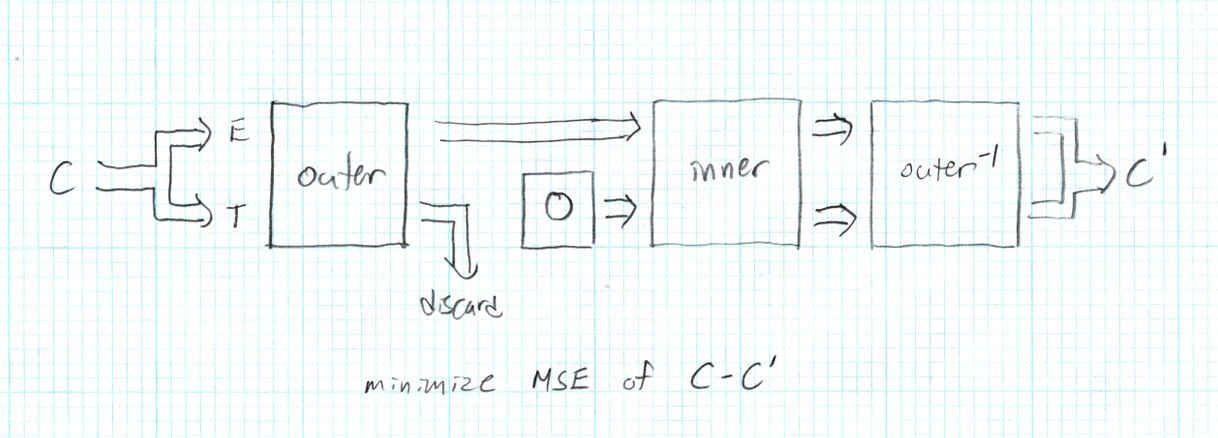
Upcoming testing goal: I'm hoping the 'outer' filter can be trained to be the same for each of our coding modes. Only 'inner' would eb mode specific. That will greatly simplify trying to infer coding mode from the coded coefficients.